Integral By Parts Example - Have you ever faced difficulties while solving integrals that involve products of functions? Well, integration by parts is the perfect technique for solving these tricky problems. In this post, we will guide you through the concept and use of integration by parts, accompanied by some helpful tips and examples.
Integration by Parts: Definite Integrals Exercises
What is Integration by Parts?
Before we dive deeper into the concept of integration by parts, let us understand what it means. Integration by parts is a technique used to integrate the product of two functions. It is essentially a way of breaking down a complicated integral into simpler components which can be solved using the basic rules of integration.
The formula for integration by parts is:
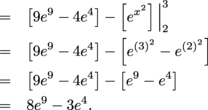
Integration by Parts: Proof
How to Derive the Formula for Integration by Parts?
The formula for integration by parts can be derived using the product rule of differentiation. Consider two functions f(x) and g(x). When we take the derivative of their product, we get:

How to solve an integral?
Using Integration by Parts to Solve Integrals
Now that we know what integration by parts is and how to derive the formula, let us focus on how to use it to solve integrals. Essentially, integration by parts is used when we have integrals of the form:

The basic steps of integration by parts are:
- Select u and dv in such a way that the product of the two functions is equal to the integral you want to solve.
- Calculate the derivative of u and integral of dv.
- Apply the formula for integration by parts.
- Solve the resulting equation for the integral.
Integration By Parts Formula: Integration By Parts Introduction
Integration by Parts Example
Let us consider an example to understand the concept of integration by parts better. We want to evaluate the integral:
We can choose:
- u = ln(x)
- dv = dx
Therefore, we get:
- du = dx/x
- v = x
Applying the formula for integration by parts, we get:
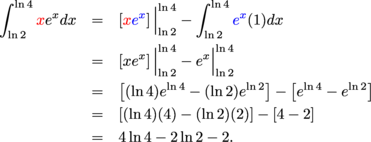
Simplifying the equation, we get:
Therefore, the solution to the integral is:
Conclusion
Integration by parts is a crucial technique in calculus that is used to solve complex integrals that involve products of functions. By understanding the concept of the formula and the basic steps to solve an integral using integration by parts, you will be able to perform more advanced calculations with ease.
We hope that this post has been helpful and informative, and that you can now use integration by parts to solve any integral thrown your way!
Find more articles about Integral By Parts Example


